Libertini - An Adaptive Theory of Aging Based on Kin Selection

 

Libertini proposed in 1988 [Libertini 1988] a theory explaining as an adaptive phenomenon, in terms of kin selection, the "increasing mortality with increasing chronological age in populations in the wild" (IMICAW) shown by many species in natural conditions and commonly defined as aging. However, he avoided purposely the term "aging", as it could cause confusion with different phenomena (e.g. the progressive increase of mortality in animals in captivity from ages not existing in the wild, a phenomenon not subject to natural selection while IMICAW, which by definition is present in the wild, is subject to it).

The hypothesis, already exposed in a previous not peer-reviewed book in Italian [Libertini 1983] and widened in subsequent works [Libertini 2006, 2008, 2009a, 2009b], may be shortly described as follows.

Disregarding the early stages of life (development and growth of the individual), which for various reasons usually have a high mortality, not necessarily correlated with the adult mortality, an IMICAW species has a life table approximately described by the Gompertz-Makeham equation [Comfort 1979] or, better, by Weibull’s equation [Ricklefs 1998]:

m_t = m₀ + α^tβ

where: t is the time; m_t is the overall mortality rate at time t; m₀, or extrinsic mortality, is the mortality at its initial lowest value (at the time defined 0 after the early stages of life); α and β are two constants and the term α^tβ is the age specific mortality, or intrinsic mortality (m_i).

For other species, defined as non-IMICAW, the mortality is constant at any age present in natural conditions [Comfort 1979; Finch 1990]:

m_t = m₀

When the derivative of the mortality exceeds an arbitrary threshold value, the time at which this occurs was defined t*. The time, after the early stages of life and before t*, when the mortality is at its lowest value, m₀, was defined as τ. Fig. 1 illustrates these definitions.

 

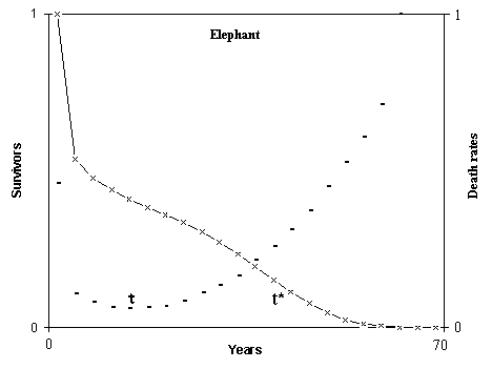
Fig. 1. Definitions of τ and t* for a mammal species. (Figure from [Libertini 1988])

Firstly, he observed that IMICAW phenomenon was documented for many species and contributed significantly to reduce the mean duration of life (ML) in wild conditions (Table 1, fig. 2 and 3)

Table 1 - HML is the hypothetical value of ML without the increment due to αt^β. The ratio HML/ML shows that the intrinsic mortality reduces significantly the ML. Excluding the ages before τ, which are not influenced by m_i, the intrinsic mortality shows a greater effect (see ratio [HML_τ-τ]/[ML_τ-τ]). (Table and references from [Libertini 1988])
 

Species	Source of data	Time unit	τ	m0	ML	HML	Ratio HML/ML	MLτ-τ	HMLτ-τ	Ratio [HMLτ-τ]/[MLτ-τ]
Zebra	1	year	6	4.63	8.48	17.23	2.03	6.73	21.55	3.20
Hippopotamus	3	year	14	1.03	15.40	43.33	2.81	21.69	96.88	4.45
Elephant	2	year	16	1.95	17.27	28.85	1.67	21.08	51.95	2.42
Waterbuck	4	year	3	5.55	3.71	9.56	2.57	4.47	18.00	4.02
Warthog	1	year	8	5.90	4.79	7.43	1.55	5.92	16.93	2.85
Impala	1	year	3	5.44	6.37	16.87	2.64	4.76	18.35	3.85
Buffalo	1	year	5	4.23	5.50	12.16	2.21	6.80	23.61	3.46
Dall mountain sheep	5	year	4	3.54	7.15	23.00	3.21	5.52	28.17	5.09
Floscularia conifera	5	day	3	7.69	5.17	11.54	2.23	3.76	12.99	3.45

Sources of data: (1) Spinage, 1972;  (2) Laws, 1966;  (3) Laws, 1968; (4) Spinage, 1970;  (5) Deevey, 1947; sex combined for all.

 

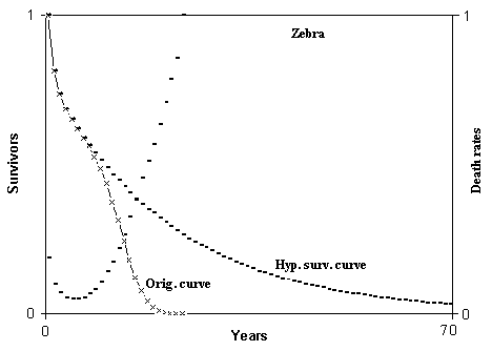
Fig. 2 - Hypothetical survival curve of zebra. Abscissas from 0 to 70 years. Calculation from 0 to 350 years. Min. mortal.: at 6 years = 4.638216%. ML = 8.480926 years; HML = 17.23965 years; ratio HML/ML = 2.032755. ML(6) = 6.730483 years; HML(6) = 21.55998 years; ratio HML(6)/ML(6) = 3.203333. (Figure from [Libertini 1988])

 

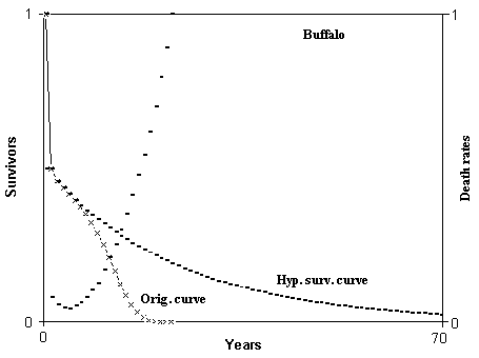
Fig. 3 - Hypothetical survival curve of buffalo. Abscissas from 0 to 70 years. Calculation from 0 to 350 years. Min. mortal.: at 5 years = 4.235282%. ML = 5.503607 years; HML = 12.16345 years; ratio HML/ML = 2.210086. ML(5) = 6.805135 years; HML(5) = 23.61117 years; ratio HML(5)/ML(5) = 3.469611. (Figure from [Libertini 1988])

Libertini observed that a smaller ML causes a quicker generation turnover and, so, a quicker diffusion of a favourable gene within a species. As the diffusion of a favourable gene C is proportional to its advantage S, he showed that an increase of S or a comparable reduction of ML have the same effects (Fig. 4)

 

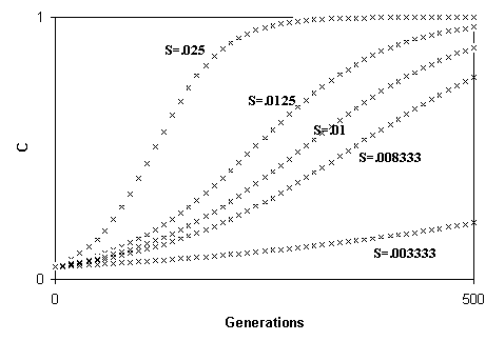
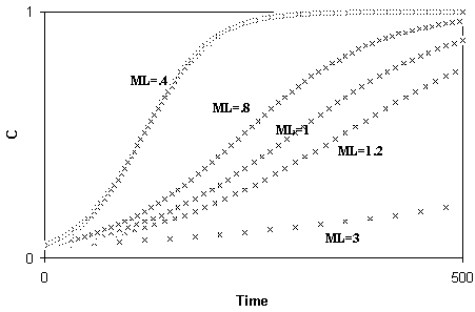
Fig. 4 - A) Spreading of a gene C according to the variation of S (while ML = k = 1); B) Spreading of a gene C according to the variation of ML (while S = k = .01). An increase of S or a proportional decrease of ML have the same effects on the spreading of C. (Figure from [Libertini 1988])

In terms of group selection, this proved that a C gene causing IMICAW was advantageous, but group selection was, and is, a very dubious argument.
It was necessary to prove that an IMICAW-causing gene, balancing and exceeding the immediate advantages of the non- (or with-tardy-) IMICAW organisms, had an immediate advantage at every generation for the genes that were supposed to induce it. Without this immediate advantage, the genes determining IMICAW would be wiped out by natural selection.

The necessary argument was formulated in terms of kin selection [Hamilton 1971; Trivers & Hare 1976; Wilson 1975].

Libertini observed that in species divided in small populations (demes) and with the number of individuals limited by ecological restraints, that is a species in conditions of K-selection, the coefficient of relationship (r) between its members is greater than the mean r of the species. This entails that in such conditions an individual pre-deceased by action of an IMICAW-causing gene is mainly substituted by a kin individual. Therefore, an IMICAW-causing gene would be favoured by natural selection if the disadvantage S' for the pre-deceased individual was less than the increment of the sum of the advantages (∑S) for kin individuals caused by the quicker turnover of generations (proportional to the ratio between the ML of a neutral allele C' and the ML determined by C; respectively ML_C' and ML_C) multiplied by r. This means that an IMICAW-causing gene is favoured by natural selection if:

r ∑S (ML_C'/ML_C - 1) > S'

This arguments led to two main predictions:

1) IMICAW phenomenon was predicted for species in conditions of K-selection. As K-selection is in general associated with territoriality and social organization, a relationship between K-selection, territoriality, social organization and IMICAW phenomenon was predicted.

2) The opposite was predicted for species in the opposite ecological conditions (r-selection) and for species without territoriality and social organizations. In such conditions the non-IMICAW condition was predicted to be common.

"That is, only for K selected species we will have survival curves of type I (see Pianka, 1970). Moreover a certain parallelism has to be observed between IMICAW and unselfish and social behaviours (Wilson, 1975, in particular Pianka's table as modified in chapter IV). This parallelism is not casual since in our theory a gene causing IMICAW is a kind of unselfish gene." [Libertini 1988]

However, the first case is widespread in mammals and birds, the second case is ordinary in reptiles, fishes and many invertebrate animals. A different interpretation of this phenomenon - without specific data in support of it - is based on the ancestry of each phylum or subphylum (historical hypothesis) [De Magalhães & Toussaint 2002].

Another important prediction was that:

3) in the case of a high extrinsic mortality (m₀), as the ML was reduced by m₀, the advantage of the action of an IMICAW-causing gene was reduced and therefore the effects of IMICAW-causing genes (alias intrinsic mortality, m_i) was predicted to be reduced, that is aging was predicted to be delayed.

This prediction, defined "Methuselah effect", was the opposite of traditional theories, which predicted a positive relation between extrinsic and intrinsic mortality: “The principal determinant in the evolution of longevity is predicted to be the level of extrinsic mortality. If this level is high, life expectancy in the wild is short, the force of selection attenuates fast, deleterious gene effects accumulate at earlier ages, and there is little selection for a high level of somatic maintenance. Consequently, the organism is predicted to be short lived even when studied in a protected environment. Conversely, if the level of extrinsic mortality is low, selection is predicted to postpone deleterious gene effects and to direct greater investment in building and maintaining a durable soma” [Kirkwood & Austad 2000].

The Methuselah effect was clearly documented by Ricklefs in an authoritative and documented review while he searched confirmations for the predictions of traditional theories [Ricklefs 1998].

From the observational data about mammal and bird life tables in the wild, Ricklefs obtained and described a very interesting relation, namely a significant (p<0.001) inverse relation between extrinsic mortality (m₀) and the proportion of deaths due to intrinsic mortality (Fig. 5).

 

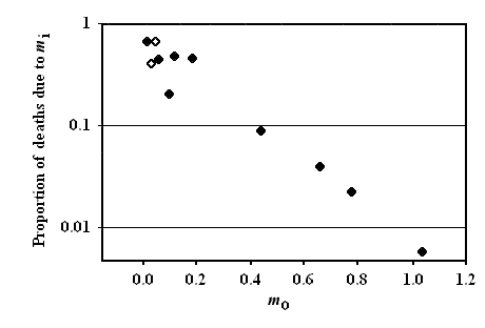
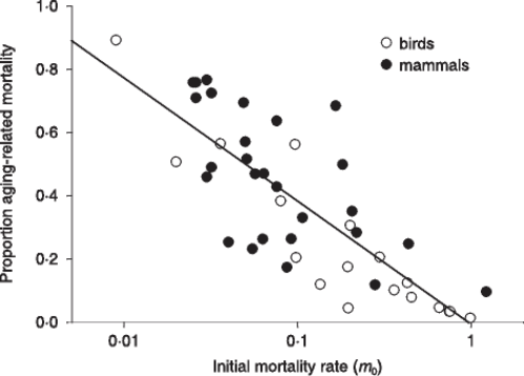
FIGURE 5 – A) Inverse significant correlation between m0 and the proportion of deaths due to mi. Data from [Ricklefs 1998], Table 2 (p. 30). Ricklefs’ fig. 7 (p. 34). The figure has been redrawn. Ordinates are in logarithmic scale. Open symbols refer to mammal species, solid symbols to bird species. B) The same of A but the figure is from [Ricklefs 2008] and is not redrawn. Moreover, open symbols refer to birds and solid symbols to mammals.

Ricklefs plainly stated in his discussion (not in the title of his paper!) that the prediction of the current theories was clearly contradicted by the inverse relation observed between m₀ and the proportion of deaths due to m_i [Ricklefs 1998]. This clear statement is omitted in his paper of paper of 2008 and no justification for the phenomenon is expressed [Ricklefs 2008]

A last and very important prediction was that:
4) if the IMICAW phenomenon is adaptive, the existence of specific mechanisms causing an age-related progressive fitness decline is essential.
This prediction is verified by the huge amount of data about the telomere-telomerase system and its actions that limit cell duplication and cell turnover, causing an age-related progressive fitness decline [Fossel 2004; Libertini 2006, 2009a].

"Finally, a ... problem is that in a deme the first copy of a C gene causing IMICAW, or a more precocious IMICAW, cannot be advantageous since there is no copy of C in other individuals that might be benefitted by its action. The answer, is probably the same as that proposed by Boorman & Levitt (1973) for unselfish genes i.e., non selective mechanisms are important up to a critical frequency." [Libertini 1988]

References:
-Comfort, A. (1979) The Biology of Senescence. Livingstone, London. [Google Scholar]
- Deevey E.S.JR. (1947) Life tables for natural populations of animals. Quart. Rev. Biol. 22, 283-314. [PubMed] [Google Scholar]
- De Magalhães, J.P. & Toussaint, O. (2002) The evolution of mammalian aging. Exp. Gerontol. 37, 769-75. [PubMed] [Google Scholar]
- Finch, C.E. (1990) Longevity, Senescence, and the Genome. University of Chicago Press, Chicago. [Google Scholar]
- Fossel, M.B. (2004) Cells, Aging and Human Disease. Oxford University Press, Oxford, USA. [Google Scholar]
- Hamilton W.D. (1971) Selection of selfish and altruistic behaviour in some extreme models. In Man and Beast: Comparative Social Behavior (Eisenberg J.F. & Dillon W.S. eds), pp. 57 91. Smithsonian Institution Press, Washington. [Google Scholar]
- Kirkwood T.B.L. & Austad S.N. (2000) Why do we age? Nature 408, 233-238. [PubMed] [Google Scholar]
- Laws R.M. (1966). Age criteria for the African elephant. E. Afr. Wildl. J. 4, 1-37. [Google Scholar]
- Laws R.M. (1968). Dentition and ageing of the hippopotamus. E. Afr. Wildl. J. 6, 19-52. [Google Scholar]
- Libertini G. (1983) [Evolutionary Arguments] [Book in Italian]. Società Editrice Napoletana, Naples (Italy). [Free]
- Libertini G. (1988) An Adaptive Theory of the Increasing Mortality with Increasing Chronological Age in Populations in the Wild. J. Theor. Biol. 132, 145-62. [PubMed] [Google Scholar] [Free]
- Libertini G. (2006) Evolutionary explanations of the “actuarial senescence in the wild” and of the “state of senility”. TheScientificWorldJOURNAL 6, 1086-1108 DOI 10.1100/tsw.2006.209. [PubMed] [Google Scholar] [Free]
- Libertini G. (2008) Empirical evidence for various evolutionary hypotheses on species demonstrating increasing mortality with increasing chronological age in the wild. TheScientificWorldJOURNAL 8, 182-93 DOI 10.1100/tsw.2008.36. [PubMed] [Google Scholar] [Free]
- Libertini G. (2009a) The Role of Telomere-Telomerase System in Age-Related Fitness Decline, a Tameable Process, in Telomeres: Function, Shortening and Lengthening (Mancini L. ed.), Nova Science Publishers Inc., 2009, New York (ISBN 978-1-60692-350-4). [Nova Science Publishers] [Free]
-Libertini G. (2009b) Prospects of a Longer Life Span beyond the Beneficial Effects of a Healthy Lifestyle, in Handbook on Longevity: Genetics, Diet & Disease (Bentely J.V. & Keller M.A. eds.), Nova Science Publishers Inc., 2009, New York (ISBN 978-1-60741-075-1). [Nova Science Publishers] [Free]
- Pianka E.R. (1970). On r- and K-selection. Amer. Natur. 104, 592-597. [Google Scholar]
- Ricklefs R.E. (1998) Evolutionary Theories of Aging: Confirmation of a Fundamental Prediction, with Implications for the Genetic Basis and Evolution of Life Span. Am. Nat. 152, 24-44. [PubMed] [Google Scholar]
- Ricklefs R.E. (2008) The evolution of senescence from a comparative perspective. Funct. Ecol. 22, 379-392. [Google Scholar] [Free]
- Spinage C.A. (1970). Population dynamics of the Uganda Defassa Waterbuck (Kobus defassa Ugandae Neumann) in the Queen Elizabeth park, Uganda. J. Anim. Ecol. 39, 51-78. [Google Scholar]
- Spinage C.A. (1972). African ungulate life tables. Ecology 53, 645-652. [Google Scholar]
- Trivers R.L. & Hare H. (1976) Haplodiploidy and the evolution of the social insect. Science 191, 249-263. [PubMed] [Google Scholar]
-Wilson E.O. (1975). Sociobiology: The New Synthesis. Harvard University Press, Cambridge. [Google Scholar]

www.programmed-aging.org

Sponsored by Azinet LLC © 2009