Medawar's Hypothesis on Mammal Aging

 

Summary: Medawar's hypothesis contended that beyond a particular age the evolutionary benefit of a longer life span in mammals was negligible. This species-specific age was greater than and proportional to the age at which the species was first capable of reproduction. Therefore aging has negligible evolutionary effect in mammals.

 

Sir Peter Medawar (1915 – 1987) was a noted British professor of zoology and anatomy at the University of London who won the Nobel Prize in medicine (1960) for his work on acquired immunological tolerances. In Medawar’s 1952 paper, An Unsolved Problem of Biology, (originally presented as a lecture at University College London) he presented an ingenious theory, which, in effect, combines the properties of the accumulation of damage theories with Weismann’s evolved characteristictheory.

 

Medawarsuggested that the force of natural selection decreases once an organism reaches an age where it has had some opportunity to reproduce. If, for example, some trait of an animal tended to be fatal prior to puberty, that trait would be very strongly selected against because most animals having that trait would die before having any progeny and would therefore not pass their adverse trait to descendents.

 

If, on the other hand, an animal had a trait which caused a fatal effect only after the animal had reached sexual maturity, survived to least one mating season, mated, had progeny, and nurtured and protected those progeny long enough for them to become self sufficient (assuming it is an animal that nurtures and protects young), the effect of that trait on fitness would be relatively insignificant. The negative trait would only affect the animal’s ability to survive yet longer and have subsequent descendents. Such a trait would apparently only weakly affect fitness. Aging seemed to fit this description.

 

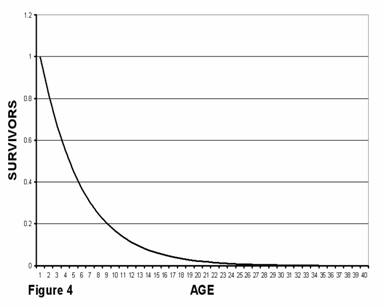
Medawar proposed that even if an animal did not age, that is, did not have an increased probability of death as a function of age, the numbers of adult animals of any given age would decrease exponentially because of deaths due to other causes such as predators, environmental conditions, etc. Some constant percentage of the animals of any given age would be killed in any given time period. As a metaphor, he used the random breaking and replacing of test tubes. If, in a lab with hundreds of test tubes, when a test tube is broken it is replaced with a new (age = 0) test tube, then after a while the number of test tubes of a given age in the test tube population will decline exponentially with age. Figure 4 shows the kind of survivor’s curve (number as a function of age) that would be expected for the test tubes (or ageless animals) as presented in Medawar’s paper. This behavior is known as an exponential decline and is characterized as having a half-life. If half of the animals die in four years (as shown here), then half of the remaining half will die in another four years, and so forth. Very old animals would be very rare even in a non-aging species.

 

 

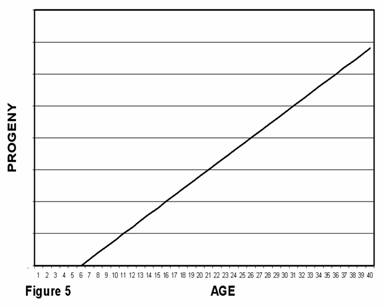
The number of progeny any given non-aging animal would produce was assumed by Medawar to increase linearly with age. An ageless animal would tend statistically to have the same number of progeny every year from puberty to death. The total number of progeny (on average) produced by animals, as a function of their age, would therefore look like Figure 5 in which total descendents produced by an animal are zero until puberty and then increase with age. Puberty is shown here as occurring at age 6. It is assumed that reproductive vigor in an ageless animal would not change with age. (We could have assumed that general reproductive effectiveness and aging were different, independent phenomena. However, an evolved characteristic that causes a decline in reproductive effectiveness has the same problems with Darwin’s mechanics as aging and the same arguments, pro and con, apply.)

 

 

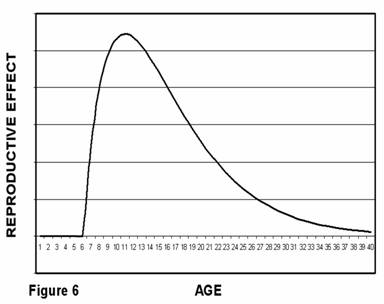
If we multiply the number of progeny produced by animals of a given age by the number of animals at that age we can determine the reproductive effect contributed by each age group or cohort. Since the number of animals is exponentially decreasing with age and the number of progeny is only linearly increasing with age, the reproductive effectof older animals (and therefore their apparent evolutionary impact) declines. Graphically, this would look like Figure 6 in which reproductive effect rises from zero at puberty to a maximum and then declines.

 

 

These curves, Figures 4-6, represent the traditional modelof a non-aging species. Medawar’s paper was almost entirely devoted to the development of this model.

 

You will note that there are no numbers specified on the vertical axes of Figures 5 and 6. Some species, subject to high death rates due to predators or other cause would need a correspondingly high birth rate to survive. Other species would need a lower birth rate.

 

Problems with Medawar's Hypothesis

 

Medawar's hypothesis depends on the idea that the evolutionary importance of individuals in a non-aging population declines with calendar age and that therefore natural selection allows the existence of progressively more negative traits with age, up to and including “death of old age.” This idea, the traditional model, is based on a very important assumption, namely, that the evolutionary contribution of each individual animal can be accurately described by “reproductive effect” as described graphically in figure 6.

 

You will recall that figure 6 reflects the combined effect of the reproductive contribution we could expect from individual animals (figure 5) and the rate at which we could expect the non-aging animals to die off (figure 4). Because the population of older animals declines more rapidly with calendar age than the reproductive contribution of older individuals increases with calendar age, the net effect (figure 6) is that evolutionary importance declines with calendar age beyond some point that varies with age of sexual maturity. This traditional model of a non-aging species is over-simplified and ignores a number of important characteristics of actual animals, all of which tend to increase the evolutionary importance of older animals.

 

First, the characteristics of Medawar’s test tubes (and non-aging animals) were presumed to be constant and did not change with the age of the test tube. However, the characteristics of actual non-aging animals would change greatly with calendar age, at least between puberty and “maturity.”

 

Suppose we had a group of prehistoric 15-year-old humans and another group of 20-year-olds. According to the reproductive effect concept, these two populations are equivalent and have the same evolutionary importance. In actuality, the 20-year-olds are superior with regard to essentially any survival characteristic. They are stronger, faster, and smarter. They would win in any competitive situation. It is obvious that a 20-year-old has a greater chance for survival than a 15-year-old, everything else being equal. Therefore, death rates would nominally tend to decline with calendar age in the interval between 15 and 20 as opposed to remaining constant as proposed by the traditional model. (In actual animals, still additional complexity such as protection-of-young might affect this.)

 

There is a more profound difficulty. The curve of figure 6 assumes that ten young individuals each producing one descendent have the same evolutionary importance as one older individual producing ten descendents. Because they are more mature, the 20-year-olds more fully exhibit adult survival characteristics. A case could therefore be made that a single 20-year-old has more evolutionary importance than any number of 15-year-olds. The reproductive effect concept does not take into account this “maturity factor.”

 

This is the same argument made against Weismann’s theory. Natural selection can not operate relative to a characteristic that is not expressed. Adult characteristics are not fully expressed in juveniles. Therefore, adults are required in order to evolve adult characteristics. Evolutionary importance is not the same as reproductive effect.

 

Second, the individuals in the population of Medawar’s test tubes were presumed to be identical and have identical characteristics. The characteristics of actual animals vary. More specifically their characteristics regarding capacity for survival vary. Therefore, their probability of survival varies.

 

The traditional model as shown in figure 4 assumes that the probability of death for an ageless animal is a constant, independent of calendar age. That is, older animals are just as likely to die in any given time period as younger animals. While true for test tubes, this idea is incompatible with the theory of natural selection. According to Darwin, animals that are more fit are less likely to die than animals that are less fit. Therefore, in any given time period, more of the less fit animals in a population would die. At the end of the period, the surviving animals would therefore, on average, be more fit than at the beginning of the period. In other words, average fitness of a non-aging population cohort increases with calendar age. Because older animals are more fit, they are also less likely to die relative to younger animals. The probability of death therefore decreases with calendar age in a non-aging population. Figure 4 therefore does not accurately represent the relative prevalence of older individuals in a population of actual non-aging animals.

 

Third, more complex animals have other characteristics that tend to increase the evolutionary importance of older animals. Mating rituals and other societal behavior traits such as those that result in “pecking order” tend to reduce the relative chance that younger animals will reproduce and in some cases also reduce the relative probability of death for older individuals.  The old king is far less likely to die in the war than the young foot soldier, especially if the old king does not age.

 

Animals learn from experience. Older non-aging animals are therefore less likely to die than genetically identical younger animals having less experience.

 

Finally, the increase in fitness with calendar age has a multiplying effect. Not only did the older individuals survive longer and have more descendants because they are more fit, but their descendents are also likely to be more fit and therefore survive longer, and their descendents descendents are likely to survive longer. This multiplication factor would appear to cause the evolutionary importance of individuals to increase exponentially with age.

 

If we attempted to modify figure 6 to develop an “evolutionary importance” curve based on these factors would it still decline with calendar age? Would the increasing evolutionary importance of older individuals compensate for their decreasing numbers?

 

It should be clear from the above discussion that the traditional model grossly underestimates the evolutionary impact of older non-aging individuals, especially in more complex organisms such as mammals. Further, the actual shape of an evolutionary importance curve is dependent on complex interactions that vary from species to species and probably even vary depending on the species’ situation regarding predators and other factors that affect life span. In effect, the traditional evolutionary theories of aging embrace the convenient aspects of Darwin’s mechanics while ignoring the inconvenient aspects.

 

Could it be that nature needs aging or other life span control mechanism to prevent a relatively few older individuals from dominating the evolutionary process?

 

These concepts are further developed in the section on evolvability theory.

 

i] Medawar, P.B, An Unsolved Problem of Biology., 1952. H.K. Lewis & Co., London.

 

www.programmed-aging.org

Sponsored by Azinet LLC © 2009